Combining like terms

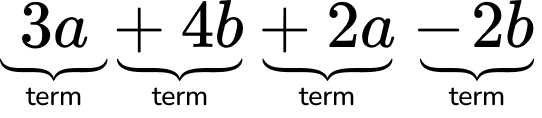
Here you will learn about combining like terms, including what a like term is and how to combine them to simplify algebraic expressions.

Students will first learn about combining like terms as part of expressions and equations in 6th grade.

What is combining like terms?

Combining like terms is a way of simplifying algebraic expressions by grouping similar parts together. When we combine like terms, we add or subtract their coefficients.

To do this, first, identify the like terms in an algebraic expression. Next, combine them by adding or subtracting. A term is a number or the product of a number and variables.

This is an expression with 4 terms.

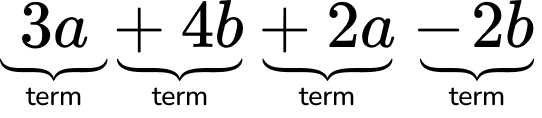
Notice the + or - sign in front of a term belongs to that term.

3a and +2a are like terms, because they are both groups of the variable a. To combine them, think about what each term represents.

Remember, when a number is next to a variable, the operation is multiplication. So, 3a is ‘3 times a’ and 2a is ‘2 times a.’

3a is 3 groups of a → +a \quad +a \quad +a

2a is 2 groups of a → +a \quad +a

Both terms are positive, so 3a + 2a = 5a.

+4b and -2b are also like terms, because they are both groups of the variable b. To combine them, think about what each term represents.

+4b is ‘4 times b’ and -2b is ‘2 times -b.’

+4b is 4 groups of b → +b \quad +b \quad +b \quad +b

-2b is 2 groups of -b → -b \quad -b

Combining +b and -b creates a zero pair, which means together they are equal to 0.

There are two zero pairs of b s, which leaves two positive b s.

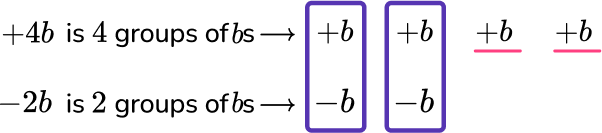
You can also think of this as 4b-2b = 2b :

Combining like terms shows that…

\begin & 3 a+4 b+2 a-2 b \\\\ & =3 a+2 a+4 b-2 b \\\\ & =5 a+2 b \end

This expression cannot be simplified further since 5a and the +2b are not like terms.

What is combining like terms?

Common Core State Standards

How does this relate to 6th grade math?

• Grade 6 – Expressions and Equations (6.EE.A.3)
  Apply the properties of operations to generate equivalent expressions.
  For example, apply the distributive property to the expression 3 \, (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 \, (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.

How to combine like terms

In order to simplify algebraic expressions by combining like terms:

1. Identify the like terms.
2. Group the like terms.
3. Combine the like terms by adding or subtracting.

[FREE] Combining Like Terms Worksheet (Grade 6)

Use this worksheet to check your 6th grade students’ understanding of combining like terms. 15 questions with answers to identify areas of strength and support!

[FREE] Combining Like Terms Worksheet (Grade 6)

Use this worksheet to check your 6th grade students’ understanding of combining like terms. 15 questions with answers to identify areas of strength and support!

Combining like terms examples

Example 1: one type of like term

Simplify the expression 3x+2x +4x .

All the terms involve groups of x. They are like terms.

2 Group the like terms.

The like terms are already grouped together.

3 Combine the like terms by adding or subtracting.

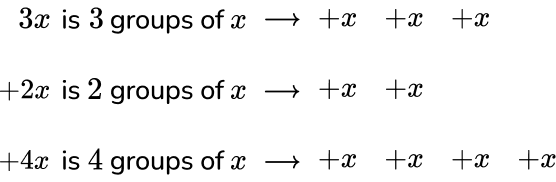
All terms are positive and there are 9 positive x s when combined, so 3x+2x +4x =9x.

Example 2: two types of like term

Simplify the expression 6a-3a +5a +5 .

Identify the like terms.

The terms involving a are like terms. The term without an a does not have any like terms.

Group the like terms.

The like terms are already grouped together.

Combine the like terms by adding or subtracting.

6a is 6 groups of a \hspace → +a \quad +a \quad +a \quad +a \quad +a \quad +a

-3a is 3 groups of -a \hspace → -a \quad -a \quad -a

+5a is 5 groups of a \hspace → +a \quad +a \quad +a \quad +a \quad +a

Combining +a and -a creates a zero pair, which means together they are equal to 0.

There are three zero pairs of a s, which leaves eight positive a s.

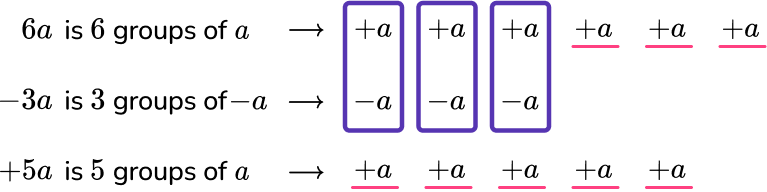
You can also think of this as subtracting 3a from 6a and then adding 5a more.

The positive and negative terms are combined to show that:

Example 3: two types of like terms

Simplify the expression 7a+4b+2a+3b.

Identify the like terms.

The terms involving a are like terms. The terms involving b are like terms.

Group the like terms.

Using the commutative property, switch the order of 4b and 2a.

Combine the like terms by adding or subtracting.

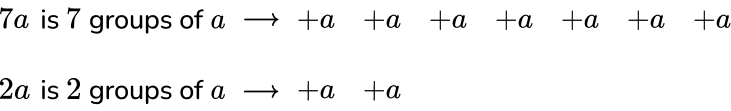
All a terms are positive, so 7a+2a =9a.

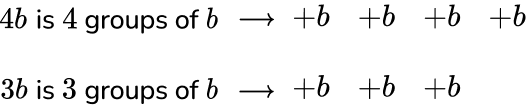
All b terms are positive, so 4b+3b =7b.

Combining all the like terms shows that:

\begin & 7 a+4 b+2 a+3 b \\\\ & =7 a+2 a+4 b+3 b \\\\ & =9 a+7 b \end

Example 4: two types of like terms

Simplify the expression -5x+4y-3x+5y.

Identify the like terms.

The terms involving x are like terms. The terms involving y are like terms.

Group the like terms.

Using the commutative property, move the 4y to the end of the equation.

Combine the like terms by adding or subtracting.

All terms are negative and there are 8 negative x s when combined, so -5x-3x = -8x.

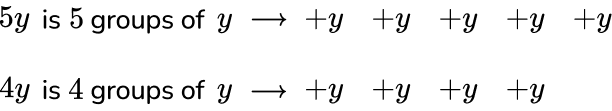
All y terms are positive, so 5y+4y =9y.

Combining all the like terms shows that:

\begin & -5 x+4 y-3 x+5 y \\\\ & =-5 x-3 x+4 y+5 y \\\\ & =-8 x+9 y \end

Example 5: three types of like terms

Simplify the expression 2c-5d+4+3c+7d+2.

Identify the like terms.

The terms involving c are like terms. The terms involving d are like terms. The terms that do not have variables are like terms, also known as constant terms.

Group the like terms.

Using the commutative property, move the ‘+ 3c’ and ‘+ 4’ next to their like terms.

2c-5d+4+3c+7d+2 = 2c+3c-5d+7d+2 + 4

Combine the like terms by adding or subtracting.

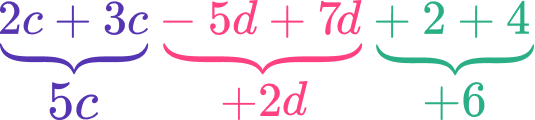
Combining all the like terms shows that:

Example 6: three types of like terms

Simplify the expression -6x+5y+4+2x-3y-7.

Identify the like terms.

The terms involving x are like terms. The terms involving y are like terms. The terms that do not have variables are like terms.

Group the like terms.

Combine the like terms by adding or subtracting.

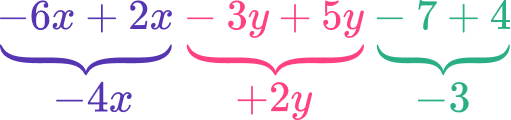
Combining all the like terms shows that:

\begin & -6 x+5 y+4+2 x-2 y-7 \\\\ = & -6 x+2 x-3 y+5y-7+4 \\\\ = & -4 x+2 y-3 \end

Teaching tips for combining like terms

• Worksheets are a useful tool to use when teaching students how to combine like terms, but ensure that students have enough room to show their solving strategy. Many worksheets do not provide enough space for students to draw out each term or use the box method. These are important strategies for students to make use of while they are learning what it means to combine like terms.

• Be sure to use different variables besides x and y when giving students examples of combining like terms. It is important that students understand that any variable can be combined with like terms.

• Use combining like terms as an introduction to creating equivalent algebraic expressions. This topic is typically easier for students to understand than using the distributive property with variables to simplify within parentheses.

• Once students have a grasp on how to combine like terms, you challenge them to take it a step further. Give students an answer key, with simplified expressions and ask them to work backwards and create the original expression. This will encourage them to think flexibly about combining like terms and show them that there are many different ways to create an original expression. However, use this only when it is an extension of this skill, since formally factoring algebraic expressions comes later.

Easy mistakes to make

• Forgetting that \bf is the coefficient if there is no number in front of a term
  If there is a letter on its own, then there is 1 of that term, but you do not need to write the number 1.

Thinking it is not possible for the answer to be zero
It is possible for all the terms to be canceled out, which results in an answer of 0 for some or all of the terms.

Thinking that unlike terms can be combined
Only like terms can be combined. This means that they have the exact same variable or no variable at all. You cannot combine variables, because they are unlike terms.

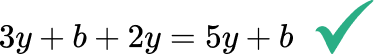
For example,

Forgetting about the commutative property
The order of the terms does not matter as long as the plus and minus signs are with the correct term.

• Not combining all the like terms
  The final answer should combine all the like terms. Carefully look at each term in the equation before writing the final answer to make sure there are none left that can be combined.

Related algebraic expression lessons

• Simplifying expressions
• Expanding expressions
• Equivalent expressions
• Evaluate the expression
• Polynomial